Metoda Simpsona
Całkowanie metodą Simpsona – jedna z metod przybliżania wartości całki oznaczonej funkcji rzeczywistej.
Metoda ma zastosowanie do funkcji stablicowanych w nieparzystej liczbie równo odległych punktów (wliczając końce przedziału całkowania). Metoda opiera się na przybliżaniu funkcji całkowanej przez interpolację wielomianem drugiego stopnia.
Znając wartości  funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
 funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
Błąd, który przy tym popełniamy, jest równy:  , gdzie:
, gdzie:
 , gdzie:
, gdzie:![c \in [x_0; x_2]](http://upload.wikimedia.org/math/4/5/8/45806695961ce8839e4585b999e8d6d4.png) .
.
Nie znamy położenia punktu c, więc posługujemy się poniższym szacowaniem, mającym zastosowanie w obliczeniach numerycznych:
![R \leqslant \frac{1}{90} h^5 \max_{x \in [x_0; x_2]} |f^{(4)}(x)|](http://upload.wikimedia.org/math/d/9/8/d98b6f6645b6f1caea5c0b00d42a7e05.png) .
.
Znając wartości funkcji w 2k+1 kolejnych, równo odległych punktach  (gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
(gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
 (gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
(gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:- ,
otrzymując:
 .
.
Wartość błędu, jakim są obarczone wyliczenia, wyraża się wzorem:
![R \leqslant \frac{1}{180} (x_n - x_0) h^4 \max_{x \in [x_0; x_n]} |f^{(4)}(x)|](http://upload.wikimedia.org/math/f/e/5/fe52b5043e9851624cba48da14ced508.png) .
.
By czytelnik mógł go odnieść do rysunku:
 ;
;  ,
, ;
;  .
.
Geometrycznie metoda ta odpowiada zastąpieniu w każdym z kolejnych k przedziałów zmiennej x łuku wykresu funkcji y=f(x) łukiem paraboli przeprowadzonej przez trzy kolejne węzły interpolacji (punkty wykresu o znanych współrzędnych) odpowiadające początkowi, środkowi i końcowi kolejnego przedziału.

 z normą
z normą  i niech
i niech  będzie podprzestrzenią liniową
będzie podprzestrzenią liniową  (elementu najlepszej aproksymacji dla danego
(elementu najlepszej aproksymacji dla danego  ), że zachodzi:
), że zachodzi:
 jest elementem "najbliższym" do aproksymowanego
jest elementem "najbliższym" do aproksymowanego  spośród wszystkich elementów
spośród wszystkich elementów  .
. .
.
 w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).


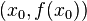
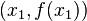
 punktów
punktów  należących do dziedziny
należących do dziedziny 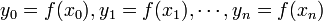
 stopnia co najwyżej
stopnia co najwyżej  takiego, że
takiego, że 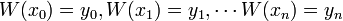 .
. znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  wartość zero.
wartość zero.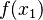 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero.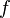 takimi, że znane są wartości
takimi, że znane są wartości 
 ,
, 

 jest wielomianem stopnia
jest wielomianem stopnia  )
) i
i  :
:
 :
:
 )
) będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej 

 .
. są równe zeru (ponieważ dla
są równe zeru (ponieważ dla  , składnik o indeksie
, składnik o indeksie  .
.
 w punktach
w punktach  i
i  stopnia
stopnia  takie same wartości.
takie same wartości.
 interpolują tę samą funkcję, to
interpolują tę samą funkcję, to  , a więc
, a więc  (węzły interpolacji są pierwiastkami
(węzły interpolacji są pierwiastkami  ).(*)
).(*) ma
ma 

 . Idealna byłaby zależność:
. Idealna byłaby zależność: ,
,![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  zależna od
zależna od 

 , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x. można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału