Metody numeryczne - Paweł Wasiak
Wikipedia
Wyniki wyszukiwania
piątek, 3 stycznia 2014
czwartek, 28 listopada 2013
Metoda Simpsona
Całkowanie metodą Simpsona – jedna z metod przybliżania wartości całki oznaczonej funkcji rzeczywistej.
Metoda ma zastosowanie do funkcji stablicowanych w nieparzystej liczbie równo odległych punktów (wliczając końce przedziału całkowania). Metoda opiera się na przybliżaniu funkcji całkowanej przez interpolację wielomianem drugiego stopnia.
Znając wartości  funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
 funkcji
funkcji  w 3 punktach
w 3 punktach  (przy czym
(przy czym  ), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale
), przybliża się funkcję wielomianem Lagrange'a i, całkując w przedziale ![[x_0,x_2]](http://upload.wikimedia.org/math/d/e/4/de4217d1fd45f2a6f7c8fa30de546aca.png) , otrzymuje przybliżoną wartość całki:
, otrzymuje przybliżoną wartość całki:
Błąd, który przy tym popełniamy, jest równy:  , gdzie:
, gdzie:
 , gdzie:
, gdzie:![c \in [x_0; x_2]](http://upload.wikimedia.org/math/4/5/8/45806695961ce8839e4585b999e8d6d4.png) .
.
Nie znamy położenia punktu c, więc posługujemy się poniższym szacowaniem, mającym zastosowanie w obliczeniach numerycznych:
![R \leqslant \frac{1}{90} h^5 \max_{x \in [x_0; x_2]} |f^{(4)}(x)|](http://upload.wikimedia.org/math/d/9/8/d98b6f6645b6f1caea5c0b00d42a7e05.png) .
.
Znając wartości funkcji w 2k+1 kolejnych, równo odległych punktach  (gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
(gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
 (gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:
(gdzie n=2k), możemy iterować powyższy wzór na kprzedziałów:- ,
otrzymując:
 .
.
Wartość błędu, jakim są obarczone wyliczenia, wyraża się wzorem:
![R \leqslant \frac{1}{180} (x_n - x_0) h^4 \max_{x \in [x_0; x_n]} |f^{(4)}(x)|](http://upload.wikimedia.org/math/f/e/5/fe52b5043e9851624cba48da14ced508.png) .
.
By czytelnik mógł go odnieść do rysunku:
 ;
;  ,
, ;
;  .
.
Geometrycznie metoda ta odpowiada zastąpieniu w każdym z kolejnych k przedziałów zmiennej x łuku wykresu funkcji y=f(x) łukiem paraboli przeprowadzonej przez trzy kolejne węzły interpolacji (punkty wykresu o znanych współrzędnych) odpowiadające początkowi, środkowi i końcowi kolejnego przedziału.
Aproksymacja
Aproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi. Często stosowana w przypadku szukania rozwiązań dla danych uzyskanych metodami empirycznymi, które mogą być obarczone błędami
Zadanie najlepszej aproksymacji
Niech dana będzie przestrzeń liniową  z normą
z normą  i niech
i niech  będzie podprzestrzenią liniową
będzie podprzestrzenią liniową  skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego
skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego  (elementu najlepszej aproksymacji dla danego
(elementu najlepszej aproksymacji dla danego  ), że zachodzi:
), że zachodzi:
 z normą
z normą  i niech
i niech  będzie podprzestrzenią liniową
będzie podprzestrzenią liniową  skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego
skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego  (elementu najlepszej aproksymacji dla danego
(elementu najlepszej aproksymacji dla danego  ), że zachodzi:
), że zachodzi:
Należy przez to rozumieć, że element  jest elementem "najbliższym" do aproksymowanego
jest elementem "najbliższym" do aproksymowanego  spośród wszystkich elementów
spośród wszystkich elementów  .
.
 jest elementem "najbliższym" do aproksymowanego
jest elementem "najbliższym" do aproksymowanego  spośród wszystkich elementów
spośród wszystkich elementów  .
.
Zadanie najlepszej aproksymacji jest zawsze rozwiązywalne tzn. dla każdego  istnieje element najlepszej aproksymacji
istnieje element najlepszej aproksymacji  , ale niekoniecznie jest on jedyny. Należy zauważyć, że element najlepszej aproksymacji zależy od normy, jaka została przyjęta w przestrzeni
, ale niekoniecznie jest on jedyny. Należy zauważyć, że element najlepszej aproksymacji zależy od normy, jaka została przyjęta w przestrzeni  .
.
 istnieje element najlepszej aproksymacji
istnieje element najlepszej aproksymacji  , ale niekoniecznie jest on jedyny. Należy zauważyć, że element najlepszej aproksymacji zależy od normy, jaka została przyjęta w przestrzeni
, ale niekoniecznie jest on jedyny. Należy zauważyć, że element najlepszej aproksymacji zależy od normy, jaka została przyjęta w przestrzeni  .
.Zadanie najlepszej aproksymacji w przestrzeniach unitarnych
Niech  będzie przestrzenią z iloczynem skalarnym i niech norma w
będzie przestrzenią z iloczynem skalarnym i niech norma w  będzie generowana tym iloczynem:
będzie generowana tym iloczynem:  .
.
 będzie przestrzenią z iloczynem skalarnym i niech norma w
będzie przestrzenią z iloczynem skalarnym i niech norma w  będzie generowana tym iloczynem:
będzie generowana tym iloczynem:  .
.
Wtedy element najlepszej aproksymacji jest jedyny i jest określony następującą tożsamością

- Aproksymacja funkcji
- Aproksymacje można wykorzystać w sytuacji, gdy nie istnieje funkcja analityczna pozwalająca na wyznaczenie wartości dla dowolnego z jej argumentów, a jednocześnie wartości tej nieznanej funkcji są dla pewnego zbioru jej argumentów znane. Mogą to być na przykład wyniki badań aktywności biologicznej dla wielu konfiguracji leków. Do wyznaczenia aproksymowanej aktywności biologicznej nieznanego leku można wówczas zastosować jedną z wielu metod aproksymacyjnych.Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga się, aby przechodziła ona przez jakieś konkretne punkty, tak jak to ma miejsce w interpolacji. Z matematycznego punktu widzenia aproksymacja funkcji
 w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  tj.
tj.  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  normy) między
normy) między  a
a  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratową i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratową i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.
wtorek, 29 października 2013
Schemat Hornera
Schemat Hornera powiązany z nazwiskiem Hornera - brytyjskiego matematyka żyjącego na przełowmie XVIII i XIX wieku. Schemat Hornera to sposób obliczania wartości wielomianu dla danej wartości argumentu wykorzystujący minimalną liczbę mnożeń. Jest to również algorytm dzielenia wielomianu W(x) przez dwumian x - c.
Schemat Hornera pozwala na wyznaczenie ilorazu Q(x) z dzielenia wielomianu
W(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0 przez dwumian x - c.
W(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0 przez dwumian x - c.
Podzielmy przez dwumian x - 5 wielomian W(x) = x3 + x2 - 10x + 8
Wykonując dzielenie za pomocą schematu Hornera tworzymy tabelkę, gdzie w górnym wierszu schematu wypisujemy współczynniki dzielnej, tzn. wielomianu x3 + x2 - 10x + 8.
| 1 | +1 | -10 | +8 | |
| +5 | 1 | +6 | +20 | (+108) |
W dolnym wierszu w pierwszej kolumnie zapisujemy liczbę odjętą od x w dzielniku. Pozostałe wartości to współczynniki ilorazu x2 + 6x + 20 oraz reszta (+108).
Wiersz dolny otrzymujemy z górnego w następujący sposób:
- pierwszy współczynnik wiersza dolnego równy jest pierwszemu współczynnikowi wiersza górnego tzn. liczbie 1,
- drugi współczynnik wiersza dolnego otrzymujemy, mnożąc poprzedni współczynnik tego wiersza, tzn. 1 przez 5 i dodając do drugiego współczynnika wiersza górnego, tzn. do +1
1 · (+5) + (+1) = +6 ,
- trzeci współczynnik wiersza dolnego otrzymujemy, mnożąc poprzedni współczynnik tego wiersza, tzn. +6 przez +5 i dodając do trzeciego współczynnika wiersza górnego, tzn. -10
(+6) · (+5) + (-10) = +20 ,
- podobnie mamy (+20) · (+5) + (+8) = +108,
- pierwszy współczynnik wiersza dolnego równy jest pierwszemu współczynnikowi wiersza górnego tzn. liczbie 1,
- drugi współczynnik wiersza dolnego otrzymujemy, mnożąc poprzedni współczynnik tego wiersza, tzn. 1 przez 5 i dodając do drugiego współczynnika wiersza górnego, tzn. do +1
1 · (+5) + (+1) = +6 ,
- trzeci współczynnik wiersza dolnego otrzymujemy, mnożąc poprzedni współczynnik tego wiersza, tzn. +6 przez +5 i dodając do trzeciego współczynnika wiersza górnego, tzn. -10
(+6) · (+5) + (-10) = +20 ,
- podobnie mamy (+20) · (+5) + (+8) = +108,
Ostatecznie możemy zapisać:
(x3 + x2 - 10x + 8) : (x - 5) = x2 + 6x + 20 reszta +108.
(x3 + x2 - 10x + 8) : (x - 5) = x2 + 6x + 20 reszta +108.
Film prezentujący zastosowanie schematu Hornera:
poniedziałek, 14 października 2013
Interpolacja wielomianowa
Interpolacja wielomianowa,
nazywana też interpolacją Lagrange'a,
od nazwiska pioniera badań nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą
numeryczną przybliżania funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami interpolacji wartości takie same jak przybliżana
funkcja.
Interpolacja
jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj
skończoną liczbą danych do określenia zależności między wielkościami.
Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x) ciągłą na przedziale domkniętym można
dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.
Interpolacja liniowa

 i
i  , dla których można utworzyć funkcję liniową, której wykres przechodzi przez punkty
, dla których można utworzyć funkcję liniową, której wykres przechodzi przez punkty 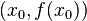 i
i 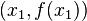 .
.Ogólna metoda
Metoda interpolacji polega na:
- wybraniu
 punktów
punktów  należących do dziedziny
należących do dziedziny  , dla których znane są wartości
, dla których znane są wartości 
- znalezieniu wielomianu
 stopnia co najwyżej
stopnia co najwyżej  takiego, że
takiego, że  .
.
Interpretacja geometryczna – dla danych  punktów na wykresie szuka się wielomianu stopnia co najwyżej
punktów na wykresie szuka się wielomianu stopnia co najwyżej  , którego wykres przechodzi przez dane punkty.
, którego wykres przechodzi przez dane punkty.
 punktów na wykresie szuka się wielomianu stopnia co najwyżej
punktów na wykresie szuka się wielomianu stopnia co najwyżej  , którego wykres przechodzi przez dane punkty.
, którego wykres przechodzi przez dane punkty.Znajdowanie odpowiedniego wielomianu
Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten sposób:
- Dla pierwszego węzła o wartości
 znajduje się wielomian, który w tym punkcie przyjmuje wartość
znajduje się wielomian, który w tym punkcie przyjmuje wartość  , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dla kolejnego węzła znajduje sie podobny wielomian, który w drugim węźle przyjmuje wartość
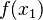 , a w pozostałych węzłach
, a w pozostałych węzłach  wartość zero.
wartość zero. - Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego
- Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym razem dodając go do wielomianu wynikowego
- Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest wielomianem interpolującym
Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu odnajdowania tego wielomianu.
Dowód istnienia wielomianu interpolującego
Niech  będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 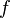 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 będą węzłami interpolacji funkcji
będą węzłami interpolacji funkcji 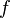 takimi, że znane są wartości
takimi, że znane są wartości 
Można zdefiniować funkcję:
 ,
, 
taką, że dla 
 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)

 jest wielomianem stopnia
jest wielomianem stopnia  (mianownik jest liczbą, a licznik iloczynem
(mianownik jest liczbą, a licznik iloczynem  wyrazów postaci
wyrazów postaci  )
)- Gdy
 i
i  :
:
- Gdy
 i
i  :
:
(licznik = 0 ponieważ występuje element
 )
)Niech
 będzie wielomianem stopnia co najwyżej
będzie wielomianem stopnia co najwyżej  , określonym jako:
, określonym jako:Dla

 .
.
Wszystkie składniki sumy o indeksach różnych od
 są równe zeru (ponieważ dla
są równe zeru (ponieważ dla  , składnik o indeksie
, składnik o indeksie  jest równy:
jest równy: .
.
A więc
z czego wynika, że  jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.
 jest wielomianem interpolującym funkcję
jest wielomianem interpolującym funkcję  w punktach
w punktach  .
.Jednoznaczność interpolacji wielomianowej
Dowód
Załóżmy, że istnieją dwa tożsamościowo różne wielomiany  i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.
Niech
 i
i  stopnia
stopnia  , przyjmujące w węzłach
, przyjmujące w węzłach  takie same wartości.
takie same wartości.Niech
będzie wielomianem. Jest on stopnia co najwyżej
 (co wynika z własności odejmowania wielomianów).
(co wynika z własności odejmowania wielomianów).Ponieważ
 i
i  w węzłach
w węzłach  interpolują tę samą funkcję, to
interpolują tę samą funkcję, to  , a więc
, a więc  (węzły interpolacji są pierwiastkami
(węzły interpolacji są pierwiastkami  ).(*)
).(*)Ale każdy niezerowy wielomian stopnia
 ma co najwyżej
ma co najwyżej  pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że
pierwiastków rzeczywistych, a ponieważ z (*) wiadomo, że  ma
ma  pierwiastków, to
pierwiastków, to  musi być wielomian tożsamościowo równy zeru. A ponieważ
musi być wielomian tożsamościowo równy zeru. A ponieważ
to
co jest sprzeczne z założeniem, że
 i
i  są różne.
są różne.Błąd interpolacji
Dość naturalne wydaje się przyjęcie, że zwiększenie liczby węzłów interpolacji (lub stopnia wielomianu interpolacyjnego) pociąga za sobą coraz lepsze przybliżenie funkcji f(x) wielomianem  . Idealna byłaby zależność:
. Idealna byłaby zależność:
 . Idealna byłaby zależność:
. Idealna byłaby zależność: ,
,
tj. dla coraz większej liczby węzłów wielomian interpolacyjny staje się "coraz bardziej podobny" do interpolowanej funkcji.
Dla węzłów równo odległych tak być nie musi → efekt Rungego.
Można dowieść, że dla każdego wielomianu interpolacyjnego stopnia  , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
 , przybliżającego funkcję
, przybliżającego funkcję  w przedziale
w przedziale ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) na podstawie
na podstawie  węzłów, istnieje taka liczba
węzłów, istnieje taka liczba  zależna od
zależna od  , że dla reszty interpolacji
, że dla reszty interpolacji 
gdzie  , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
 , a
, a ![\xi \in [a;b]](http://upload.wikimedia.org/math/f/1/3/f1302a366e78b319c24f828cebac3bdc.png) jest liczbą zależną od x.
jest liczbą zależną od x.
Do oszacowania z góry wartości  można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu  .
.
 można posłużyć się wielomianami Czebyszewa stopnia
można posłużyć się wielomianami Czebyszewa stopnia  do oszacowania wartości
do oszacowania wartości  dla
dla ![x\in [-1,1]](http://upload.wikimedia.org/math/5/4/7/547db7d2339cfb3345123313fe6a4981.png) . Dla przedziału
. Dla przedziału ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) wystarczy dokonać przeskalowania wielomianu
wystarczy dokonać przeskalowania wielomianu  .
.
Subskrybuj:
Posty (Atom)









